안녕하세요 '코딩 오페라'블로그를 운영하고 있는 저는 'Conducter'입니다.
오늘 알아볼 내용은 K-평균 알고리즘(K-means clustering algorithm)입니다.
K-평균 알고리즘(K-means clustering algorithm)은 주어진 데이터를 k개의 클러스터로 묶는 알고리즘으로, 각 클러스터와 거리 차이의 분산을 최소화하는 방식으로 동작한다. 이 알고리즘은 자율 학습의 일종으로, 레이블이 달려 있지 않은 입력 데이터에 레이블을 달아주는 역할을 수행한다.
K-평균 알고리즘(K-means clustering algorithm)은 원하는 클러스터의 수를 정해주면 이 숫자만큼 아래 그림과 같이 클러 시터 링을 해줍니다. 이때 클러스터링 하는 기준은 아래 그림처럼 SSE(Sum of Squared Errors) 즉 에러들의 합이 가장 작게 하는 것입니다.
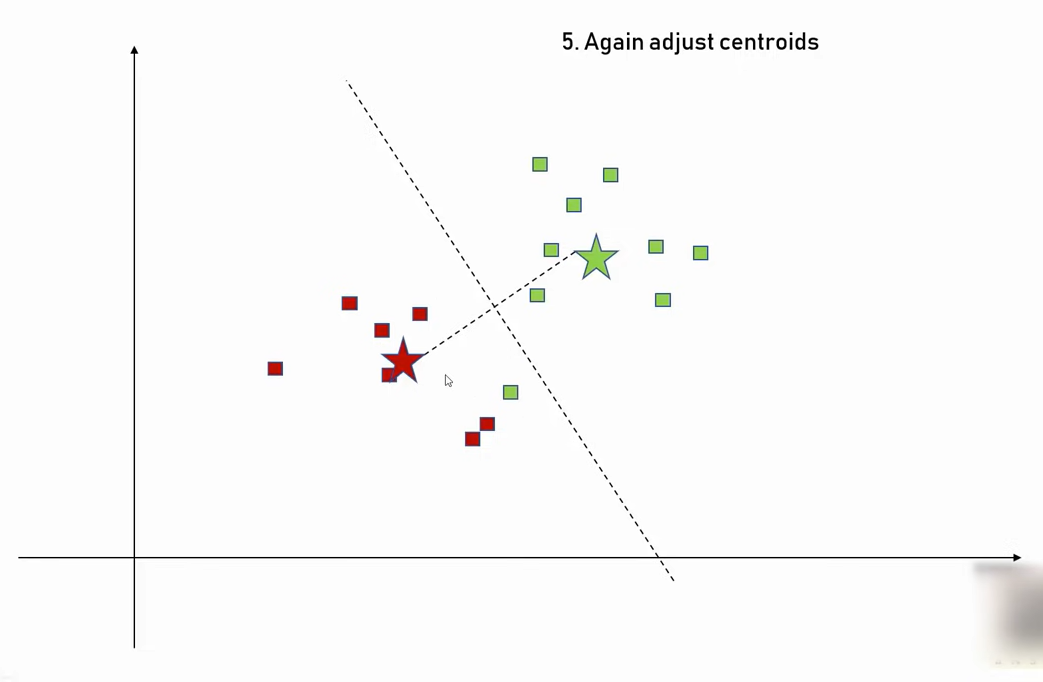

그러면 클러스터링 수는 어떻게 정해야 될까요? 이는 Elbow Technique을 사용하면 됩니다. 이는 아래 그림과 같이 그래프가 팔모양일때 팔꿈치에 해당하는 점이 클러스터링 개수를 의미한다는 것입니다. 즉 그래프의 기울기의 변화가 가장 심한 점이 클러스터링 수를 나타냅니다.

그러면 지금부터는 간단한 예시를 통해 K-means clustering algorithm을 알아보도록 하겠습니다. 이번 예시는 나이와 수입에 따른 클러스터링 입니다. 먼저 기본적인 라이브러리를 불러옵니다. 여기서 sklearn의 KMeans와 MinMaxScaler 알고리즘을 불러와주는데, KMeans는 K-means clustering algorithm을, MinMaxScaler는 모든 데이터를 0에서 1로, 즉 최대 1, 최소 0으로 정규화 시켜주는 알고리즘입니다. 이렇게 정규화를 하는 이유는 더욱 학습이 잘 되게 하기 위해서입니다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.preprocessing import MinMaxScaler
icome csv를 불러와 데이터 프레임을 만들어줍니다. 그다음 MinMaxScaler알고리즘을 사용하여 Age와 Income을 정규화해줍니다.
df = pd.read_csv('income.csv')
scaler = MinMaxScaler()
df['Income($)'] = scaler.fit_transform(df[['Income($)']])
# Income($)을 정규화
df['Age'] = scaler.fit_transform(df[['Age']])
# Age을 정규화
클러스터 개수를 정해주고 클러스터를 예측해줍니다. 이렇게 예측된 클러스터 값을 데이터 프레임에 추가해줍니다.
km = KMeans(n_clusters = 3)
# 클러스터 개수를 정해준다.
y_predicted = km.fit_predict(df[['Age', 'Income($)']])
# 클러스터를 예측
df['cluster'] = y_predicted
# 클러스터를 데이터에 추가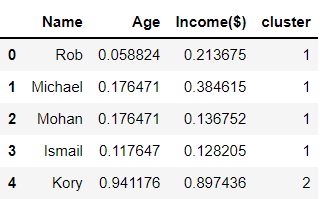
. cluster_centers_함수를 이용하여 각 클러스터의 중간값을 찾아줍니다.
km.cluster_centers_
# 각 클러스터의 중심값array([[0.1372549 , 0.11633428],
[0.85294118, 0.2022792 ],
[0.72268908, 0.8974359 ]])
클러스터 된 값들과 각 클러스터의 중간값들을 색깔을 달리 하여 그래프로 나타내 줍니다.
df1 = df[df.cluster == 0]
df2 = df[df.cluster == 1]
df3 = df[df.cluster == 2]
# 각 클러스터의 데이터프레임을 분류
plt.scatter(df1.Age, df1['Income($)'], color = 'green')
plt.scatter(df2.Age, df2['Income($)'], color = 'red')
plt.scatter(df3.Age, df3['Income($)'], color = 'black')
plt.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:, 1], color = 'purple', marker = '*', label = 'centroid')
# 각 클러스터의 중심값을 지정
plt.xlabel('Age')
plt.ylabel('Income($)')
plt.legend()
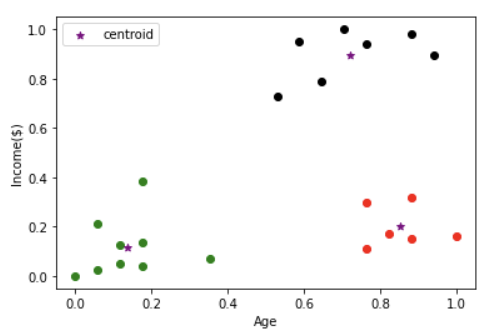
위에서 우리는 클러스터 개수를 임의로 3개로 지정하였습니다. 그럼 이것이 최적의 개수인지 알아봅시다. 위에서 최적의 클러스터수는 SSE 즉 에러들의 제곱의 합이 가장 작을 때라고 하였습니다. 클러스터수를 1에서 10으로 잡고 각각의 SSE를 구해주는 코드를 만들면 아래와 같습니다.
k_rng = range(1, 10)
sse = []
for k in k_rng:
km = KMeans(n_clusters = k)
km.fit(df[['Age', 'Income($)']])
sse.append(km.inertia_)
# inertia_: Sum of squared distances of samples to their closest cluster center.
여기서 구한 sse값을 출력하면 아래와 같습니다.
sse[5.434011511988179,
2.091136388699078,
0.4750783498553097,
0.3491047094419566,
0.2621792762345213,
0.21055478995472496,
0.17473586079225922,
0.1397684499538816,
0.10497488680620906]
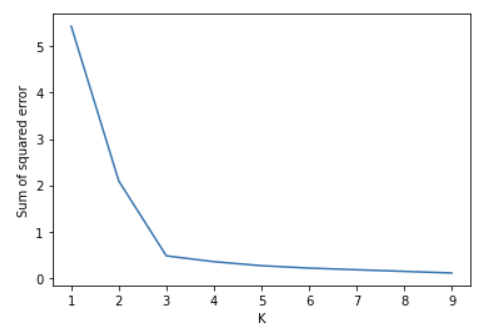
가시성을 높이기 위해 이를 그래프로 그리면 아래와 같습니다. Elbow Technique에 의해 기울기가 가장 많이 변하는 3이 클러스터 개수가 됨을 확인할 수 있습니다.
plt.xlabel('K')
plt.ylabel('Sum of squared error')
plt.plot(k_rng, sse)
# Elbow Technique에 의해 클러스터의 수가 3일때 가장 에러가 적다.
오늘은 K-평균 알고리즘(K-means clustering algorithm)에 대해 알아보았습니다. 도움이 되셨나요? 만약 되셨다면 구독 및 좋아요로 표현해 주시면 정말 많은 힘이 됩니다. 궁금한 사항 혹은 앞으로 다루어 주었으면 좋을 주제가 있으시면 댓글 남겨주시면 감사하겠습니다. 저는 '코딩 오페라'의 'Conductor'였습니다. 감사합니다.
<출처 및 참고 : 위키백과, code basics>
'머신러닝' 카테고리의 다른 글
| 나이브 베이즈 분류 알고리즘(Naive Bayes Classifier Algorithm), 스팸메일 예측(Spam Mail) (0) | 2022.01.27 |
|---|---|
| 나이브 베이즈 분류 알고리즘(Naive Bayes Classifier Algorithm), 타이타닉 생존자 예측 (0) | 2022.01.27 |
| Support Vector Machine(SVM) (0) | 2022.01.20 |
| 로지스틱 회귀(Logistic Regression) (2) | 2022.01.12 |
| 학습 데이터와 훈련 데이터(Training Data and Testing Data) (0) | 2022.01.12 |