안녕하세요 '코딩 오페라'블로그를 운영하고 있는 저는 'Conducter'입니다.
오늘 알아볼 내용은 로지스틱 회귀(Logistic Regression)입니다.
로지스틱 회귀(Logistic Regression)
로지스틱 회귀(Logistic Regression)는 회귀를 이용하여 데이터가 어떤 범주에 속할 확률을 0에서 1 사이의 값으로 예측하고 그 확률에 따라 가능성이 더 높은 범주에 속하는 것으로 분류해주는 지도 학습 알고리즘입니다.
예를들어 나이와 보험유무를 알수 있는 데이터가 있다고 해봅시다. 선형회귀 를 사용하면 아래와 같은 그래프가 그려집니다. 실제 데이터는 y값은 0에서 1인 반면 예측된 모델은 -무한대에서 +무한대 까지인것을 알 수 있습니다.

그럼 로지스틱 회귀를 사용하면 어떨까요? 아래 그림은 로지스틱 회귀를 사용하여 학습한 그래프입니다. 이제야 예측 모델이 확률 0에서 1사이에 있고 실제 값과도 더욱 잘 맞는것을 알 수 있습니다. 이러한 이유로 로지스틱 회귀를 사용합니다.

Sigmoid Function(시그모이드 함수)
로지스틱 회귀에서 가장 많이 사용하는 함수로, 0부터 1까지의 확률을 가능하게 해주는 함수 입니다.
Sigmoid Function(시그모이드 함수)은 다음과 같이 생겼습니다.

$$sigmoid(z) = \frac{1}{1 + e^{-z}}$$
지금부터는 예제를 통해 로지스틱 회귀(Logistic Regression)를 알아보도록 합시다.
우선 필요한 라이브러리를 불러와줍니다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
#머신러닝 분석에 유용한 라이브러리
from sklearn.linear_model import LogisticRegression
#LogisticRegression: 시그모이드 함수
from sklearn.model_selection import train_test_split
그 다음 나이에 따른 보험유무 데이터를 불러줍니다.
df = pd.read_csv('insurance_data.csv')
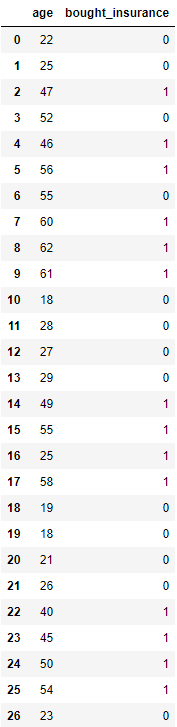
train_test_split함수를 사용하여 Test data와 Train data를 분리해줍니다. 아래 코드의 경우 Test data = 10%, Train data = 90%입니다.
X_train, X_test, y_train, y_test = train_test_split(df[['age']], df.bought_insurance, test_size = 0.1)
로지스틱 회귀(Logistic Regression)로 모델을 만들어주고 Train data로 모델을 학습시켜줍니다.
model = LogisticRegression()
model.fit(X_train, y_train)
그 다음 '.predict'함수를 이용하여 값을 예측해주고, 최종적으로 '.score'함수를 통해 모델이 잘 맞는지 확인해줍니다. 이 경우 score이 '1' 즉 100%로 상당히 잘 학습된것을 알 수 있습니다.
model.predict(X_test)
model.score(X_test, y_test)
오늘은 '로지스틱 회귀(Logistic Regression)'에 대해 알아보았습니다. 도움이 되셨나요? 만약 되셨다면 구독 및 좋아요로 표현해 주시면 정말 많은 힘이 됩니다. 저는 '코딩 오페라'의 'Conductor'였습니다. 감사합니다.
<출처 및 참고 : 위키백과, code basics>
'머신러닝' 카테고리의 다른 글
| K-평균 알고리즘(K-means clustering algorithm) (0) | 2022.01.20 |
|---|---|
| Support Vector Machine(SVM) (0) | 2022.01.20 |
| 학습 데이터와 훈련 데이터(Training Data and Testing Data) (0) | 2022.01.12 |
| 선형 회귀 모델의 수학적 해석(Gradient Descent and Cost Function) (0) | 2022.01.11 |
| 다변수 선형 회귀(Linear Regression Multiple Variables) (0) | 2022.01.10 |