안녕하세요 '코딩 오페라'블로그를 운영하고 있는 저는 'Conducter'입니다.
오늘 알아볼 내용은 선형 회귀 모델의 수학적 해석입니다.
선
수학에서 우리가 흔히 알고 있는 선은 변수, 기울기, 절편으로 이루어진 'y = mx + b'꼴입니다. 여기서 m은 기울기로 'slope'을 의미하고, b는 y절편으로 'intercept'을 의미합니다.
Cost Function(비용 함수)
흔히 '가성비가 좋다'라는 말은 성능대비 비용이 적을 때 하는 말이죠? 선형 회귀 알고리즘도 마찬가지입니다. 비용이 적을수록 성능이 좋습니다. 이러한 비용을 함수로 나타낸 것을 Cost Function(비용 함수)라고 합니다.
MSE(평균 제곱 오차, Mean Squared Error)
위 Cost Function(비용 함수)의 종류 중 하나로 오차들을 제곱한 값을 평균 낸 값을 의미합니다. 여기서 제곱을 하는 이유는 값을 모두 양수로 만들기 위함입니다. 수식으로 나타내 주면 아래와 같습니다.

Gradient Descent
여기서 우리는 Cost Fuction 즉, MSE값이 가장 작게 하도록 하는 m(slope), b(intercept)를 찾아야 하는데, 이런 방식을 Gradient Descent라고 합니다.

그러면 어떻게 하면 가장 작은 MSE를 찾을 수 있을까요? 위 그림에 힌트가 있습니다. 이차함수에서 가장 작은값은 기울기가 '0'일 때입니다. 그러면 이 값을 수식으로 구해봅시다.
Gradient Descent for Intercept(절편)
$$L = \frac{1}{N}\sum_{i=1}^{n}(y_{i} - \hat {y}_{i})^{2}$$
$$= \frac {1}{N}\sum_{i=1}^{n}(y_{i} - (mx_{i} + b))^{2}$$
$$\frac {dL}{db} = \frac {-2}{N}\sum_{i=1}^{n}(y_{i} - (mx_{i} + b))$$
Loss를 b로 미분해주면 위와 같은 값이 됩니다. 이를 다시 파이썬 코드로 나타내 주면 다음과 같습니다. 참고로 여기서 y는 참값을, y헷은 예측값을 의미합니다.
def gradient_for_b(x, y, m, b):
diff = sum([y_i - (m * x_i + b) for x_i, y_i in zip(x, y)])
b_gradient = diff * (-2 / len(x))
return b_gradient
Gradient Descent for slope(기울기)
$$\frac {dL}{dm} = \frac {-2}{N}\sum_{i=1}^{n}(y_{i} - (mx_{i} + b))(x_{i})$$
이번에는 Loss를 m으로 미분해주면 위와 같은 값이 됩니다. 이를 다시 파이썬 코드로 나타내 주면 다음과 같습니다.
def gradient_for_m(x, y, m, b):
diff = sum([x_i * (y_i - (m * x_i + b)) for x_i, y_i in zip(x, y)])
m_gradient = diff * (-2 / len(x))
return m_gradient
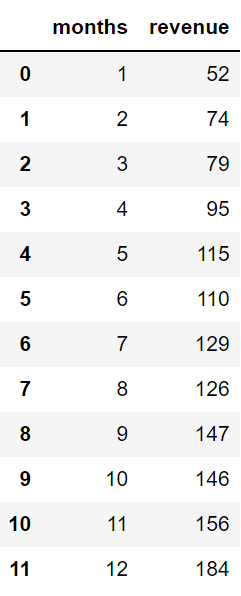
이해를 돕기 위해 이를 이용한 예제를 알아보도록 하겠습니다. 예제는 월별 수익을 예측하는 모델을 만드는 것입니다.
먼저 필요한 라이브러리를 불러와줍니다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
그다음 사용할 데이터 csv파일을 불러와 줍니다.
df = pd.read_csv('monthly_revenue.csv')
위에서 언급했던 b에 관한 기울기와 m에 관한 기울기 함수를 정의해줍니다.
def gradient_for_b(x, y, m, b):
diff = sum([y_i - (m * x_i + b) for x_i, y_i in zip(x, y)])
b_gradient = diff * (-2 / len(x))
return b_gradientdef gradient_for_m(x, y, m, b):
diff = sum([x_i * (y_i - (m * x_i + b)) for x_i, y_i in zip(x, y)])
m_gradient = diff * (-2 / len(x))
return m_gradient
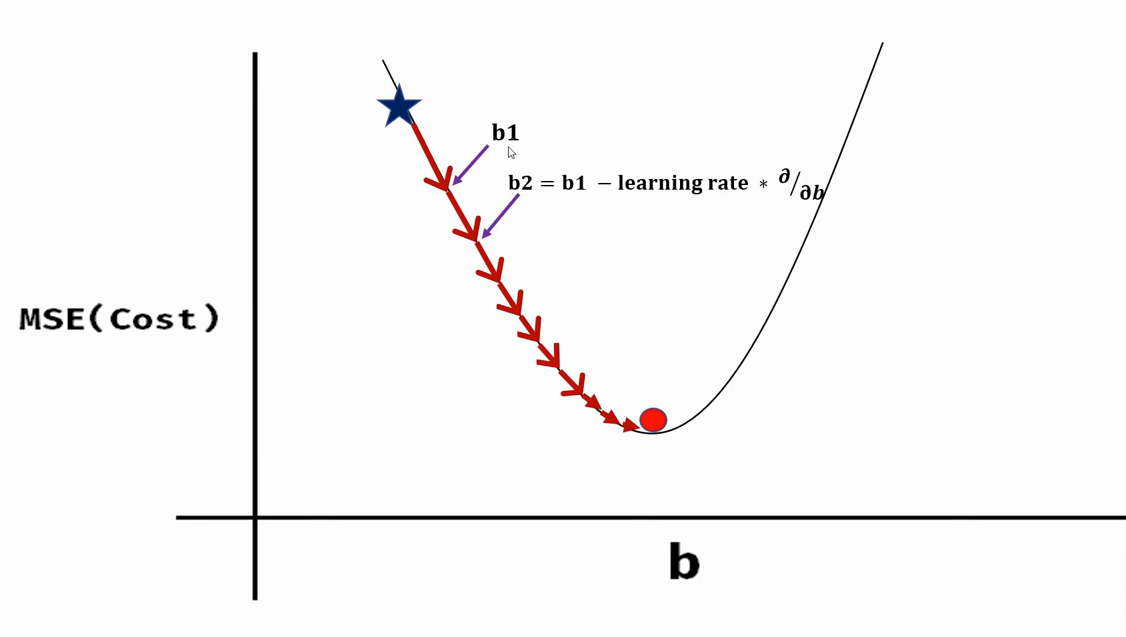
위의 그림과 같이 스텝에 따라 b와 m값을 계속 업데이트해줍니다. 업데이트 방식은 다음과 같습니다.
b2 = b1 - learning_rate * d/db
m2 = m1 - learning_rate * d/dm
여기서 learning rate앞에 '-'부호가 붙은 이유는 수학적으로 gradient의 반대 방향에 최솟값(기울기가 '0')이 존재하기 때문입니다.
이를 다시 파이썬 함수로 나타내면 다음과 같습니다.
def step_gradient(x, y, m_current, b_current, learning_rate):
b_gradient = gradient_for_b(x, y, m_current, b_current)
m_gradient = gradient_for_m(x, y, m_current, b_current)
b = b_current - (learning_rate * b_gradient)
m = m_current - (learning_rate * m_gradient)
return [b, m]
여기에 스탭을 반복해서 학습시켜주는 함수를 추가해주면 아래와 같습니다. 여기서 학습과정을 알아보기 쉽게 하기 위해. 학습을 100번 할 때마다 m, b, cost값을 프린트해주는 기능을 추가했습니다.
def gradient_descent(x, y, learning_rate, num_iteration): #interation(반복)
m, b = 0, 0
#m, b를 '0'으로 초기화
for i in range(num_iteration):
b, m = step_gradient(x, y, b, m, learning_rate)
x = np.array(x)
y = np.array(y)
#numpy로 만들어줘야 m * x행렬연산가능
y_predicted = m * x + b
cost = (1 / len(x)) * sum([val ** 2 for val in (y - y_predicted)])
if i % 100 == 0:
print("b = {}, m = {}, cost = {}".format(b, m, cost))
return [b, m]
learning rate = 0.01, iteration(반복, 학습 스탭수) = 1000으로 하고 학습을 시켜주면, 아래와 같이 학습이 잘 되는 모습을 알 수 있습니다.
b, m = gradient_descent(df.months, df.revenue, 0.01, 1000)
y = [m*x + b for x in df.months]
plt.scatter(df.months, df.revenue)
plt.plot(df.months, y, color='orange')

위의 코드들은 아래 제 github링크에 있으니 참고하시기 바랍니다.
GitHub - CodingOpera/ML
Contribute to CodingOpera/ML development by creating an account on GitHub.
github.com
오늘은 '선형 회귀 모델의 수학적 해석'에 대해 알아보았습니다. 도움이 되셨나요? 만약 되셨다면 구독 및 좋아요로 표현해 주시면 정말 많은 힘이 됩니다. 저는 '코딩 오페라'의 'Conductor'였습니다. 감사합니다.
<출처 및 참고 : 위키백과, code basics>
'머신러닝' 카테고리의 다른 글
| Support Vector Machine(SVM) (0) | 2022.01.20 |
|---|---|
| 로지스틱 회귀(Logistic Regression) (2) | 2022.01.12 |
| 학습 데이터와 훈련 데이터(Training Data and Testing Data) (0) | 2022.01.12 |
| 다변수 선형 회귀(Linear Regression Multiple Variables) (0) | 2022.01.10 |
| 단변수 선형 회귀(Linear Regression Single Variable) (0) | 2022.01.10 |