안녕하세요 '코딩 오페라'블로그를 운영하고 있는 저는 'Master.M'입니다. 현재 저는 '초등학생도 이해하는 자연어 처리'라는 주제로 자연어 처리(NLP)에 대해 포스팅을 하고 있습니다. 제목처럼 진짜 핵심 내용을 쉽게 설명하는 것을 목표로 하고 있으니 자연어 처리(NLP)에 입문하고 싶은 분들은 많은 관심 부탁드립니다. 이번 시간에 알아볼 내용은 'Big Bird: Transformers for Longer Sequences' 논문입니다.
Abstract
- Transformer 구조는 현재 NLP에서 가장 혁신적인 구조로 가장 성능이 좋음
- 그럼에도 불구하고 연산량이 문장의 길이의 제곱(quadratic) 하게 된다는 단점을 가지고 있음
- 이 논문에서는 이러한 이차원 적인 연산량을 선형적(일차원)으로 줄이는 모델을 제안함
BIGBIRD Architecture

BigBird 모델은 기존 Transformer의 attention 연산량 문제를 해결하기 위해 Random, Window, Global attention 개념을 도입함
- Random Attention : 기존의 모든 단어간 연관도를 계산한 attention 메커니즘과 달리 단어들을 random 하게 샘플링하여 연산량을 줄이는 방법. 이를 위해 'small world graph'를 사용.

- Clustering Coefficient
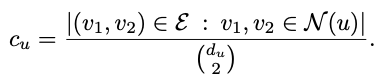
Clustering Coefficient는 해당 노드에 이웃하는 노드들이 얼마나 잘 연결되었는지를 평가하는 지표로 수식은 위와 같음. 여기서 d_v는 노드 v의 degree를 뜻하는 것으로 해당 노드 v가 몇개의 인접노드들과 연결되었는지를 나타냄. N(v)는 노드 v의 인접노드들을 뜻함. 따라서 clustering coefficient = 1이면 인접 노드들이 모두 서로 연결되어 있고, clustering coefficient = 0이면 인접 노드들이 모두 서로 연결되어있지 않은 상태.

예시를 들어 이해를 해보자. 위와 같은 그래프가 있을때 clustering coefficient의 분모는 4C2 = 6이 됨.(노드 v와 연결된 인접노드들이 4개 이므로, d_v=4이기 때문) 분자는 인접노드들끼리 연결된 선의 수가 3개 이므로 3이 됨. 따라서 최종적으로 clustering coefficient는 3/6 = 0.5가 됨.
- Erdos-Rényi random graph
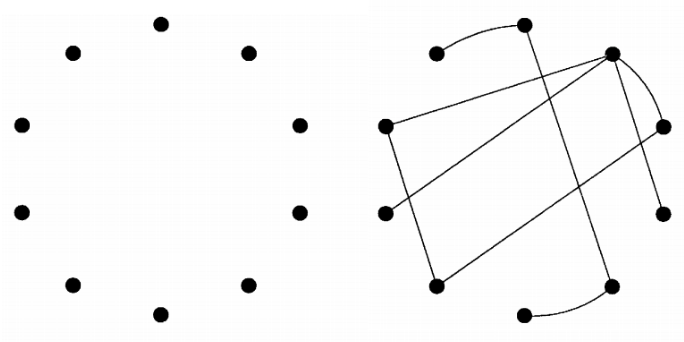
랜덤 그래프의 한 종류로 처음에 각 노드들 연결쌍 마다 0 ~ 1 사이수를 랜덤 하게 주고 설정해 준 p값보다 작은 연결쌍들을 activation 해줌. 따라서 설정값 p가 커질수록 위와 같이 연결된 노드쌍 수가 확률적으로 증가. 최근 노드 간 거리가 log(n)으로 짧고(n = 노드의 수), rapid mixing time이 장점임.
- Small World Graph

Small World Graph란 몇사람만 건너면 전 세계사람들과 연결할 수 있다는 SNS이론 중 하나로, 어떤 점들이 서로를 연결할 때 아주 규칙적인 경우와 무작위 적인 경우가 아닌, 규칙성과 불규칙성을 가진 연결관계로 만들어진 네트워크를 의미함.
위 그림과 같이 그래프가 규칙성과 불규칙성의 중간정도에 위치하고 있어 노드간 접근성과 연결성이 모두 좋음.
이 논문에서는 random attention으로 'Small World Graph'를 사용하여 Erdos-Rényi random graph 대비 clustering coefficient를 증가시켰음.
- Window Attention : 문서의 길이가 길어지면 멀리 떨어진 단어들보다 가까이에 있는 단어들의 연관도가 높을 수밖에 없음. 때문에 이를 반영하고자 본 논문에서는 특정 윈도의 크기만큼의 부분에서 attention을 수행하는 'window attention'기법을 적용함.
- Global Attention

위에서 제안한 두가지 Random과 Window attention기법을 적용하면 위 표에서와 같이 Original attention에 비해 성능이 좋지 않음. 이는 기존에 비해 attention 연산수가 많이 줄어든 결과임. 때문에 이를 극복하고자 'Global Attention'기법이 제안됨.
Global Attention 기법은 새로운 'global token'을 만들 이 이 토큰이 모든 단어토큰들과 attention 하여 연결하는 것을 의미. 여기서 'global token'을 어떻게 정의하느냐에 따라 종류가 달라짐.
- BIGBIRD-ITC(Internal Transformer Construction) : 이미 존재하는 일부 토큰들을 global token으로 설정
- BIGBIRD-ETC(Extended Transformer Construction) : BERT의 CLS 토큰과 같이 새로운 global token을 지정
Experiments: Natural Language Processing

위와같이 BIGBIRD-ETC 모델이 다른 기존의 모델 및 ITC 모델보다 성능이 좋았음
Conclusion
이 논문에서는 BIGBIRD라는 희소 attention(sparse attention)을 이용하여 긴 문서에서 기존의 original attention보다 계산량도 줄이고 성능도 계선하였음.
지금 까지 저희는 'Big Bird: Transformers for Longer Sequences'에 대해 알아보았습니다. 도움이 되셨나요? 만약 되셨다면 구독 및 좋아요로 표현해 주시면 정말 많은 힘이 됩니다. 궁금한 사항 혹은 앞으로 다루어 주었으면 좋을 주제가 있으시면 댓글 남겨주시면 감사하겠습니다. 저는 '코딩 오페라'의 'Master.M'이었습니다. 감사합니다.
Reference
https://arxiv.org/abs/2007.14062
Big Bird: Transformers for Longer Sequences
Transformers-based models, such as BERT, have been one of the most successful deep learning models for NLP. Unfortunately, one of their core limitations is the quadratic dependency (mainly in terms of memory) on the sequence length due to their full attent
arxiv.org
https://m.blog.naver.com/sw4r/221258754223
[Complexity] Erdos Renyi (ER) 네트워크란?
ER Network 라고 부르는 네트워크에 대해서 간략하게 알아보자. 1. N개의 고립된 노드들로 시작한다. ...
blog.naver.com
https://process-mining.tistory.com/152
Clustering Coefficient 설명 (그래프의 clustering coefficient 계산)
이번 글에서는 node degree, node centrality에 이어 또다른 node feature인, 해당 노드에 이웃하는 노드들이 얼마나 잘 연결되어 있는지를 표현하는 지표인 clustering coefficient가 무엇인지에 대해 설명하겠다
process-mining.tistory.com
6단계면 모든 세상 사람들을 알 수 있다 - 작은 세상 효과(Small world effect) - 케빈 베이컨의 6단계
학부시절 SNS를 이용한 정보가 퍼지는 속도에 대해 시뮬레이션을 해본적이 있습니다. 이때 실제 사람들...
blog.naver.com
'자연어처리(NLP)' 카테고리의 다른 글
| ALBERT: A LITE BERT FOR SELF-SUPERVISED LEARNING OF LANGUAGE REPRESENTATIONS 논문 리뷰 (0) | 2023.05.19 |
|---|---|
| REFORMER: THE EFFICIENT TRANSFORMER (0) | 2023.05.17 |
| 4. 단어 수준 임베딩 (NPLM, Word2Vec, FastText, 잠재 의미 분석, Glove, Swivel) [초등학생도 이해하는 자연어처리] (0) | 2023.04.10 |
| 2. 자연어처리 임베딩 종류 (BOW, TF-IDF, n-gram, PMI) [초등학생도 이해하는 자연어처리] (0) | 2023.04.08 |
| 1. 자연어처리 임베딩 [초등학생도 이해하는 자연어처리] (2) | 2023.04.07 |